
They both have same height,
let the height of both triangles be = x
let the base one triangle = y
then the base of another trainlgle = 2y
Area of triangle = 1/2 X B X H
Area of Triangle 1
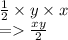
Area of Triangle 2
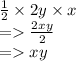
Difference in the area =

Hence Area of Triangle 1 is half the area of Triangle 2
Difference of 1/2 area.