Question

Given the sequence, 26, 13, 6.5, ..... find a) the 10th term and b) the sum of the first 18 terms X Clear * Undo Redo ​

Answer 1

`T_(10) = 0.05078125`

`S_(18) = 51.9998016358`

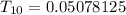
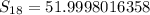
Explanation:

Given:

Sequence = 26, 13, 6.5 ....

Solving (a): The 10th term

The sequence is a geometric progression and the nth term will be solved using:

`T_n = ar^(n-1)`

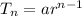
In this case:

`n = 10`

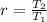`r = (T_2)/(T_1)` --- Common Ratio

`r = (13)/(26)`

`r = 0.5`

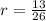
`a = 26` --- First term

So,
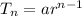`T_n = ar^(n-1)` becomes

`T_(10) = 26 * 0.5^(10-1)`

`T_(10) = 26 * 0.5^(9)`

`T_(10) = 26 * 0.001953125`

`T_(10) = 0.05078125`

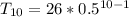
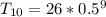
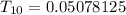
Solving (b): The sum of first 18 terms

This will be calculated using:

`S_n = (a(1 - r^n))/(1 - r)`

Substitute values for n, a and r

`S_(18) = (26 * (1 - 0.5^(18)))/(1 - 0.5)`

`S_(18) = (25.9999008179)/(0.5)`

`S_(18) = 51.9998016358`

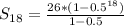
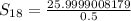
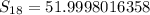
Hence, the sum of first 18 terms is 51.9998016358