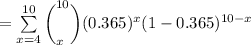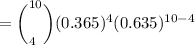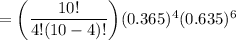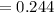Question

In each month, the proportion of ‘Prize’ bonds that win a prize is 1 in 11,000. There is a large number of prizes and all bonds are equally likely to win each prize.

(a) Show that, for a given month, the probability that a bondholder with
5000 bonds wins at least one prize, is 0.365, correct to 3 significant figures.

(b) For a given month, find the probability that, in a group of 10 bondholders
each holding 5000 bonds, four or more win at least one prize

Answer 1

Explanation:

Given that:

The proportion of price bonds that wins a prize is 1 in 111000

The probability of winning at least one prize = 1 - Probability of winning no prize at all.

Probability of winning at least one prize =
`1 - \bigg ((10999)/(11000) \bigg)^(5000)`

Probability of winning at least one prize = 1 - 0.9999090909⁵⁰⁰⁰

Probability of winning at least one prize = 1 - 0.635

Probability of winning at least one prize = 0.365

Since this question follows a binomial distribution with the probability of p = 0.365 and number of sample n = 10

Then; the probability of four or more will win at least one prize can be computed as follows:

`= \sum \limits ^(10)_(x=4) \bigg( ^(10)_(x) \bigg)(0.365)^x (1- 0.365)^(10-x)`

`= \bigg( ^(10)_(4) \bigg)(0.365)^4 (0.635)^(10-4)`

`= \bigg( (10!)/(4!(10-4)!) \bigg)(0.365)^4 (0.635)^(6)`

`= 0.244`