Question

A rock is dropped (from rest) off a bridge over the Merrimack River. The falling rock

accelerates at 10 m/s2 downward. If it takes 2.5 seconds before a splash is heard,
approximately how high is the bridge?

Answer 1

31 meters

hope it help you

thanks for free points.........

Answer 2

31.25 meters or ~31 meters approximately

Step-by-step explanation:

Let's see which of the 5 variables we are given since this is a constant acceleration problem.

• 
  `v_i \ \ \ \ \ \ t \\ v_f \ \ \ \ \ \triangle x \\ a`

We want to find the height of the bridge, aka the vertical displacement of the rock. Let's set the upwards direction to be positive and the downwards direction to be negative.

We are told that the acceleration is 10 m/s² downward, so we have a = -10 m/s².

We are also told that the time it takes the rock to hit the water is 2.5 seconds. Time is the same regardless of the x- or y- direction, so we can say that t = 2.5 seconds.

Now, we aren't told this directly, but we can figure out that the velocity in the y-direction is 0 m/s, since the rock is dropped from rest off the bridge. Therefore,
`v_i=0 (m)/(s)`.

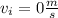We want to find the vertical displacement, the height of the bridge, so we can say that
`\triangle x= \ ?`

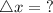
We have 4 out of 5 variables:

• 
  `v_i,\ a, \ t, \ \triangle x`

Look through the constant acceleration equations to see which equation has all 4 of these variables. You should come up with this one (no final velocity):

• 
  `x_f=x_i+v_it+(1)/(2)at^2`

Subtract
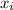`x_i` from both sides of the equation to get:

• 
  `\triangle x=v_it+(1)/(2)at^2`

Substitute in our known variables and solve for delta x.

• 
  `\triangle x=(0(m)/(s))(2.5s) + (1)/(2) (-10(m)/(s^2))(2.5s)^2`

0 m/s multiplied by 2.5 s is 0, so we have:

• 
  `\triangle x =(1)/(2) (-10)(2.5)^2`

Evaluate the exponent first and multiply the terms together.

• 
  `\triangle x =(-5)(6.25)`
• 
  `\triangle x =-31.25`

The vertical displacement is -31.25 meters from the rock's starting position, so we can say that the height of the bridge is 31.25 meters, which is approximately 31 meters tall.