Question

Which expression can be used to find the price of a $400 telescope after a 32% markup? Select all that apply.

A. 400 • 0.32
B. 400 • 3.2
C. 400 • 1.32
D. 400 + 400(0.32)
E. 400 • 400(1.32)

Answer 1

Expressions C and D correctly determine the markup price.

Explanation:

A markup in mathematics is when an object's price is raised by a certain percentage. Therefore, because we are told that the telescope is originally $400 and is marked up by 32%, we can actually mathematically evaluate this.

When you markup a price, you multiply the original price by
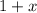`1+x`, where x is the percentage at which the object is marked up. However, x needs to be in decimal form for it to work out.

`(32)/(100) = \small\boxed{0.32}`

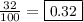
Therefore, with this new decimal, we can add 1 to it.

`1 + 0.32=\small\boxed{1.32}`

Finally, we multiply this result by the original price.

`1.32 * 400=\small\boxed{528}`

Therefore, we can already confirm that Expression C is one way to find the markup price.

• We can eliminate expression A because it did not use the formula
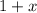  `1+x`. It only uses the decimal form of the percentage.
• We can eliminate expression B because the division to convert from the percentage form to the decimal form is flawed (the expression divided by 10 instead of 100) and also forgot to add 1 to the determined value.

Now, we can test the math for expressions D and E to see if either of these will equal $528.

Expression D is basically saying to add 32% of 400 to the original price. This would work out because we marked up the original price by 32%. Therefore, we can confirm that Expression D is also an expression that can be used to determine the markup price.

`400 + 400(0.32)\\400(0.32) = 128\\400 + 128 = \small\boxed{528}`

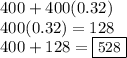
Finally, we also need to check expression E. This expression is saying to add the already marked up price to 400. This would not be correct.

`400 * 400(1.32)\\400(1.32) = 528\\400 * 528 = \small\boxed{\$ 211,200}`

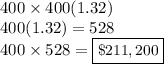
Therefore, it has been determined that Expression C & Expression D are both equations that will find a markup price.