Answer:
The 6 names to circle are:
- Laverna
- Alfonso
- Autumn
- Ignacio
- Kathyrn
- Lawrence
The underlined letters from those circled names are:
- RN
- ON
- TU
- G
- RN
- WR
The letters form the phrase
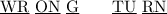 or "wrong turn". The spacing is done like that in the first version to show the various subgroups of letters.
or "wrong turn". The spacing is done like that in the first version to show the various subgroups of letters.
Unfortunately the mentioned riddle at the bottom is cut off, so I don't know what the riddle is.
======================================================
Step-by-step explanation:
- Laverna is correct because a translation is applied. "Translation" in geometry settings means "shifting up/down/left/right". In this case, triangle JKL is shifted 5 units right and 3 units up.
- Alfonso is correct. If a figure is labeled ABCD going in clockwise orientation, then a translation will preserve said orientation. The orientation only flips when a reflection occurs.
- Autumn is correct. Why? Because reflections are isometries, meaning they preserve distances and lengths and angles. In other words, the two triangles are twin clones of each other.
- Willa is not correct. The prime notations go on the image and NOT the preimage. In other words, the prime notations go for the "after" and not the "before". Example: triangle JKL in Laverna's diagram is the preimage, while J'K'L' is the image. JKL is "before", and J'K'L' is "after".
- Ignacio is correct. The figure enlarges or shrinks (depending on the scale factor if its larger than 1, or smaller than 1). The orientation stays the same. Refer to Alfonso's scenario where I mentioned the orientation flipping only when a reflection happens.
- Napoleon is incorrect. A reflection ALWAYS changes the orientation. Consider a triangle ABC where the motions from A to B to C goes clockwise. A reflection will flip the orientation to make A to B to C go counterclockwise. Example: Reflections over non-horizontal lines swap the positions of left vs right, which is another way to see why the orientation swaps as well.
- Kathyrn is correct assuming no reflection operations are done.
- Titus is not correct. A rotation is not the same as a reflection. Though I should point out that two reflections simplify to a rotation. The mirror lines must intersect in some way. Parallel mirror lines will have two reflections lead to a translation.
- Lawrence is correct. The order P,Q,R is clockwise, and so is the order P', Q', R'. A rotation preserves orientation. In this case, a 180 degree rotation has been done. The rule for that is any (x,y) point turns into (-x,-y).
Here's a summary table:

Put another way, here are the people to circle (i.e. the people who made true statements):
- Laverna
- Alfonso
- Autumn
- Ignacio
- Kathyrn
- Lawrence
In the order presented above, the letters underlined are:
- RN
- ON
- TU
- G
- RN
- WR
Through a bit of trial and error, the letters make the phrase of:
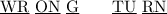
I'm not sure what to do with the extra "RN". It might be a typo, or it might be the case your teacher wants you to ignore repeats like this.