Question

Kayla's school is selling tickets to the annual dance competition. On the first day of ticket sales the school

sold 3 senior citizen tickets and 5 child tickets for a total of $70. The school took in $216 on the second day by
selling 12 senior citizen tickets and 12 child tickets. Find the price of a senior citizen ticket and the price of a
child ticket.

Answer 1

senior ticket = $10 child's ticket = $8

Explanation:

s = senior ticket

c = child's ticket

We need to write 2 equations, and we have 2 unknowns, s and c.

3s + 5c = $70

12s + 12c = $216

First solve for s using the first equation.

3s + 5c = 70 Subtract 5c from each side

3s + 5c - 5c = 70 - 5c

3s = 70 - 5c Divide each side by 3

3s/3 = (70 - 5c)/3

s =
`(70 - 5c)/(3)`

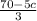
Now plug in s into the second equation.

12s + 12c = 216

12(
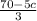`(70 - 5c)/(3)`) + 12c = 216

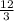`(12)/(3)` (70 - 5c) + 12c = 216

4 (70 - 5c) + 12c = 216

280 - 20c + 12c = 216

280 - 8c = 216 Add 8c to each side

280 - 8c + 8c = 216 + 8c

280 = 216 + 8c Subtract 216 from each side.

280 - 216 = 216 - 216 + 8c

280 - 216 = 8c

64 = 8c Divide each side by 8

64/8 = 8c/8

64/8 = c

8 = c

Now plug c into the first equation and solve for s.

3s + 5c = 70

3s + 5(8) = 70

3s + 40 = 70 Subtract 40 from each side.

3s + 40 - 40 = 70 - 40

3s = 70 - 40

3s = 30 Divide each side by 3

3s/3 = 30/3

s = 30/3

s = 10

So a senior ticket costs $10 and a child's ticket costs $8.