A set of coordinates that would make the proof easier to complete is: d. (0,4), (0,0), (3,0).
In Mathematics and Geometry, Pythagorean's theorem is an Euclidean postulate that can be modeled or represented by the following mathematical equation:
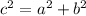
Where:
- a is the opposite side of a right-angled triangle.
- b is the adjacent side of a right-angled triangle.
- c is the hypotenuse of a right-angled triangle.
In order to determine the length of c, we would have to apply Pythagorean's theorem as follows;

c = 5 units.
Since these coordinates (0,4), (0,0), (3,0) consist of an ordered pair that is located at the origin (0, 0) with only positive integers, it represents a set of coordinates that would make the proof easier to complete.
Complete Question:
A right triangle with leg lengths of 4 and 3 units has to be positioned in the coordinate plane to write a coordinate proof.
Which set of coordinates would make the proof easier to complete?
a. (4,0), (0,0), (4,3)
b. (3,0), (0,0), (-4,0)
c. (0,4), (0,0), (-3,0)
d. (0,4), (0,0), (3,0)