Question

Find x step by step (10 points)

Answer 1

`\boxed{\left \{ {{√((n-m)(m+n))} \atop {-√((n-m)(m+n))}} \right.}`

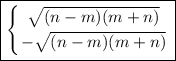
Solution Steps:

- Steps using the quadratic formula -

______________________________

1.) Subtract n² from both sides:

• 
  `n^2-n^2=0`

• 
  `m^2-n^2=m^2-n^2`

2.) Rewrite:

This equation is in standard form: ax² + bx² + c = 0. Substitute 1 for a, 0 for b, and (m-n) (m+n) for c in the quadratic formula,
`\frac{-b\frac{+}{}√(b^2-4ac) }{2a}`:

• 
  `x^2+m^2-n^2=0`

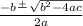2.a) Turns into:

• 
  `x=\frac{0\frac{+}{}√(0^2-4(m-n)(m+n))}{2}`

3.) Square 0:

• 
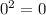  `0^2=0` (Also means it Cancels out.)

4.) Take the square root of −4(m−n)(m+n):

This just means combine them by squaring.

• 
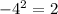  `-4^2=2` (Half it, don't square it.)

• 
  `(m-n)(m+n)^2=(n^2-m^2)`

4a.) Our equation should look like this now:

• 
  `x=\frac{0\frac{+}{}2√((n^2-m^2))}{2}`

5.) Solve the equation using ±:

Solve the equation
`x=\frac{0\frac{+}{}2√((n^2-m^2))}{2}`:

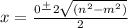5a.) Solve the equation when ± is plus:

• 
  `x=√((n-m)(m+n))`

5b.) Solve the equation when ± is minus:

• 
  `x=-√((n-m)(m+n))`

______________________________

Hope this helps!

If you have any questions, or need help with anything else, feel free to ask! I'm happy to help!

- TotallyNotTrillex -

Answer 2

`√((n-m)(n+m))` &
`-√((n-m)(n+m))`

Explanation:

1) Subtract
`m^(2)` from both sides. This should leave you with
`x^(2)=n^(2)-m^(2)`.

2) Square root both sides. This should leave you with
`x=√(n^2-m^2)` &
`x=-√(n^2-m^2)`.

You can stop here if this is what the problem is asking for. However, it is not fully simplified.

3) Factor the equation. This should leave you with
`√((n-m)(n+m))` &
`-√((n-m)(n+m))`.