Question

Help please ;-; The values in the table represent a linear function.

x 1 2 3 4
f(x) −3 −1 1 3
What is the function rule?

Write the rule in function notation, using the slope-intercept form of a line.

Enter your answer in the box.

Answer 1

The function rule in slope-intercept form is:

`y = (1)/(2)x-(7)/(2)`

Explanation:

The slope-intercept form of a function is given as:

`y = mx+b`

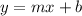
Here

m is the rate of change of function and b is the y-intercept

The rate of change is calculated as:

`m = (difference\ in\ y)/(difference\ in\ x)`

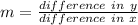
For this, any two pairs of input and output can be taken.

So using the pairs (1,-3) and (2,-1)

`m=(2-1)/(-1+3)\\=(1)/(2)`

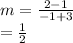
Putting the value of slope in slope-intercept form

`y = (1)/(2)x+b`

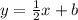
Putting (1,-3) in the equation

`-3 = (1)/(2)(1)+b\\-3 = (1)/(2)+b\\b = -3-(1)/(2)\\b = (-6-1)/(2)\\b= (-7)/(2)`

Putting the value of b

`y = (1)/(2)x-(7)/(2)`

Hence,

The function rule in slope-intercept form is:

`y = (1)/(2)x-(7)/(2)`