Question

Y=x^2-6x+3 help write the vertex form of the equation

Answer 1

`y=(x-3)^2-6`

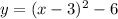
Explanation:

`y=x^2-6x+3`

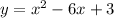
This is written in the standard form of a quadratic function:

`y=ax^2+bx+c`

where:

• ax² → quadratic term
• bx → linear term
• c → constant

You need to convert this to vertex form:

`y=a(x-h)^2+k`

where:

• (h,k) → vertex

To find the vertex form, you need to find the vertex. For this, use the equation for axis of symmetry, since this line passes through the vertex:

`x=-(b)/(2a)`

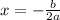
Using your original equation, identify the a, b, and c terms:

`a=1\\\\b=-6\\\\c=3`

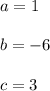
Insert the known values into the equation:

`x=-((-6))/(2(1))`

Simplify. Two negatives make a positive:

`x=(6)/(2) =3`

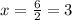
X is equal to 3 (3,y). Insert the value of x into the standard form equation and solve for y:

`y=3^2-6(3)+3`

Simplify using PEMDAS:

`y=9-18+3\\\\y=-9+3\\\\y=-6`

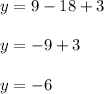
The value of y is -6 (3,-6). Insert these values into the vertex form:

`(3_(h),-6_(k))\\\\y=a(x-3)^2+(-6)`

Insert the value of a and simplify:

`y=(x-3)^2-6`

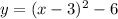
:Done