Answer:
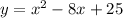
Explanation:
To answer this question, we will work backwards.
We know that a factor is 4+3i. This means that:
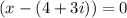
Hence, we will eliminate the imaginary and convert this into standard form.
First, distribute the negative:

Add 3i to both sides:
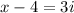
Square both sides:

Expand:
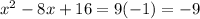
Add 9 to both sides:
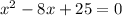
Hence, our quadratic equation is:
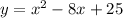
Notes:
We will get the same equation if we use (4-3i). This is because we square the (3i) regardless of its sign, making it positive.