Question

Solve the following System Of Equations Using Substitution or Elimination Methods. Show Work.

y = x2 + 3

y = x + 5

Answer 1

There are two pairs of solutions: (2,7) and (-1,4)

Explanation:

We will use substitution.

y = x^2 + 3

y = x +5

Since the second equation is equal to y, replace y in the first equation with the second equation.

y = x^2 + 3

x + 5 = x^2 + 3

Rearrange so that one side is equal to 0.

5 - 3 = x^2 - x

2 = x^2 - x

0 = x^2 - x - 2

You may use quadratic formula or any form of factoring to find the zeros (x values that make the equation equal to 0).

a = 1, b = -1, c = -2

Zeros =
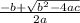`\frac{-b + \sqrt{b^(2)-4ac } }{2a}` and
`\frac{-b - \sqrt{b^(2)-4ac } }{2a}`

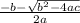
Zeros = 2 and -1

Now that you have your x values, plug them into the equations to find their corresponding y values.

y = x^2 + 3

y = (2)^2 + 3

y = 7

Pair #1: (2,7)

y = x^2 + 3

y = (-1)^2 + 3

y = 4

Pair #2: (-1,4)

Therefore, there are two pairs of solutions: (2,7) and (-1,4).