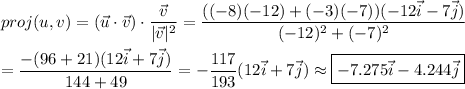Answer:
(b) -7.275i -4.244j
Explanation:
The projection of vector u onto vector v is the product of the unit vector v, the magnitude of vector u, and the cosine of the angle between them.
__
The dot product gives the product of the magnitudes of the two vectors and the cosine of the angle between them. To find the projection, we must divide the dot product by the magnitude of v and multiply by the unit vector in the direction of v.