Answer:
Reasons:
1. Given
2. Given
3. Definition of bisector
4. Reflexive property
5. SAS Congruence
Explanation:
This is quite easy to solve. All that you're expected to do is to complete the reason that justifies each statement given in the two-column proof.
Let's complete the proof as follows:
1. Statement:
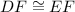
1. Reason: Given
We know this statement is true because we are given in the question.
2. Statement: FG bisects <DFE
2. Reason: Given
We also know this because we are told so in the question, as shown in the diagram given.
3. Statement:

3. Reason: Definition of bisector
We know this because an angle bisector divides an angle into two equal halves. Therefore, the definition of bisector justifies why it was stated that

4. Statement:

Reason: Reflexive property.
5. Statement: ∆DFG
 EFG
EFG
5. Reason: SAS Congruence
Two sides (DF and FG) and an included angle (angle 1) of ∆DFG is congruent two corresponding sides (EF and FG) and an included angle (angle 2) of ∆EFG. Therefore, ∆DFG
 EFG by the Side-Angle-Side (SAS) Congruence Theorem.
EFG by the Side-Angle-Side (SAS) Congruence Theorem.