Question

If z = 1 –StartRoot 3 EndRoot i, what is z^3? please help im stressed

a) -8

b) 8

c) -8i

d) 8i

Answer 1

A

Explanation:

just finished test

Answer 2

Correct answer: a) -8

Explanation:

Complex Numbers

A complex number z in polar form is expressed as

`z=r(\cos\theta+\mathbf{i}\sin\theta)`

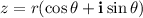
The nth power of a complex number in polar form is:

`z^n=r^n(\cos(n\theta)+\mathbf{i}\sin(n\theta))`

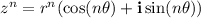
If the complex number is given in rectangular form

`z=x+\mathbf{i}y`

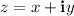
then the values of r and θ are given by:

`r=√(x^2+y^2)`

`\displaystyle \theta=\arctan\left((y)/(x)\right)`

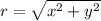
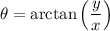
The given complex number is:

`z=1-\mathbf{i}√(3)`

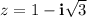
The value of r is:

`r=\sqrt{1^2+(-√(3))^2}`

`r=√(1+3)=2`

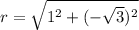
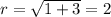
r=2

Calculating the angle:

`\displaystyle \theta=\arctan\left((-√(3))/(1)\right)`

`\displaystyle \theta=\arctan(-√(3))`

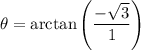
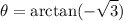
Since the number is in the quadrant IV, the angle is:

`\theta=-60^\circ`

Thus, z is expressed in polar form as:

`z=2(\cos(-60^\circ)+\mathbf{i}\sin(-60^\circ))`

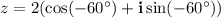
Calculating:

`z^3=2^3(\cos(-180^\circ)+\mathbf{i}\sin(-180^\circ))`

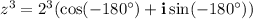
Given cos 180°=-1 and sin(-180°)=0

`z^3=8(-1+0)`

`z^3=-8`

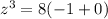
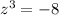
Correct answer: a) -8