Answer:
Avery is right, because
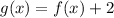 .
.
Cindy is right, because
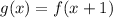 .
.
Explanation:
Let
 and
and
 functions, then
functions, then
 is the vertical translated version of
is the vertical translated version of
 if and only if:
if and only if:
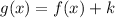 ,
,
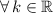
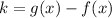
If we know that
 and
and
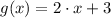 , then:
, then:
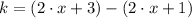
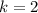
Then, Avery is right, because
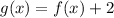 .
.
Let
 and
and
 functions, then
functions, then
 is the horizontal translated version of
is the horizontal translated version of
 if and only if:
if and only if:
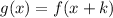 ,
,
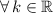
If we know that
 and
and
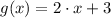 , then:
, then:
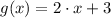
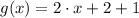
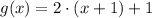
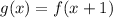
Then, Cindy is right, because
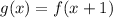 .
.