Question

How long does it take $500 to double at a simple interest rate of 24%?

Answer 1

4 years and 2 months

Explanation:

Simple interest formula

A = P(1 + rt)

where:

• A = final amount
• P = principal amount
• r = interest rate (in decimal form)
• t = time (in years)

Given:

• A = $500 × 2 = $1,000
• P = $500
• r = 24% = 0.24

Substitute the given values into the formula and solve for t:

`\implies \sf 1000 = 500(1 + 0.24t)`

`\implies \sf (1000)/(500)=(1 + 0.24t)`

`\implies \sf 2=1 + 0.24t`

`\implies \sf 1 = 0.24t`

`\implies \sf t=(1)/(0.24)`

`\implies \sf t=4 (1)/(6) \:years`

`\implies \sf t=4\:years\:2\:months`

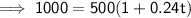
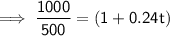
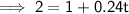
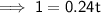
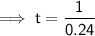
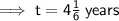
Therefore, it takes 4 years and 2 months for the initial investment of $500 to double at a simple interested rate of 24%.