Question

A converging meniscus lens has an index of refraction of 1.55 and radii of curvature for its surfaces of 4.60 cm and 9.20 cm. The concave surface is placed upward and filled with carbon tetrachloride (CCl4), which has n = 1.46. What is the focal length of the CCl4-glass combination?

Answer 1

To calculate the focal length of a CCl4-glass lens combination, use the modified lensmaker's equation considering the indices of refraction and the radii of curvature. Plug in the values, perform the calculation, and take the reciprocal of the result to obtain the focal length.

Step-by-step explanation:

To find the focal length of the combination of a converging meniscus lens and carbon tetrachloride (CCl4), we must apply the lensmaker's equation. The standard form of the lensmaker's equation for a lens in a medium other than air is:

`\( (1)/(f) = (n_(lens) - n_(medium)) \left( (1)/(R_1) - (1)/(R_2) \right) \)`

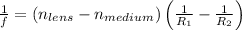
In this case, the index of refraction of the lens (glass) is 1.55, the medium (CCl4) has an index of refraction of 1.46, and the radii of curvature are 4.60 cm and 9.20 cm. Accounting for the orientation of the lens, these radii should have opposite signs since one is convex (positive) and the other is concave (negative regarding the incident light). Therefore, we compute the focal length as follows:

`\( (1)/(f) = (1.55 - 1.46) \left( (1)/(-4.60 cm) - (1)/(9.20 cm) \right) \)`

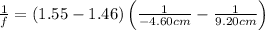
After solving for
`\( (1)/(f) \)` cal to find the focal length. The computed value will be the focal length of the CCl4-glass combination. It is important to remember that units must be consistent, so when performing the calculation, ensure all measurements are in the same unit (cm in this case).

Answer 2

Answer: the focal length of the CCl4-glass combination is 102.31 cm

Step-by-step explanation:

Given that;

Index of refraction n1 = 1.55

carbon tetrachloride (CCl4), which has n2 = 1.46

radii of curvature for its surfaces R1 = 4.6cm and R2 = 9.20 cm

the focal length of the CCl4-glass combination = ?

we can determine the focal length using the Formula;

1/f = ( n1 - n2) ( 1/R1 - 1/R)

so we substitute in our values

1/f = ( 1.55 - 1.46 ( 1/4.6 - 1/9.20)

1/f = 0.09 × 0.1086

1/f = 0.009774

f = 1 / 0.009774

f = 102.31 cm

Therefore the focal length of the CCl4-glass combination is 102.31 cm