Question

Find the future value of an ordinary annuity of $200 paid quarterly for 6 years, if the interest rate is 10%, compounded quarterly. (Round your answer to the nearest cent.)

Answer 1

Future value is $1543.12

Explanation:

From the question, present value = $200, rate = 10%, years = 6.

So that future value of ordinary annuity can be calculated by,

FV =
`\frac{A{[(1+r)^(n) - 1]}}{r}`

where: FV is the future value, A is the annuity, r is the rate, and n is the number of years.

FV =
`(200[(1+0.1)^(6)-1] )/(0.1)`

=
`(200[1.1^(6)- 1] )/(0.1)`

=
`(200*0.771561)/(0.1)`

=
`(154.3122)/(0.1)`

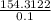
FV = $1543.122

The future value of the ordinary annuity is $1543.12.