Answer:
The total kinetic energy is 2.8m J. (NOTE: m is mass of the sphere)
Step-by-step explanation:
The total kinetic energy of a sphere is given by the sum of the rotational kinetic energy and the translational kinetic energy. That is,
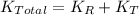
The rotational kinetic energy
 is given by
is given by
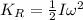
Where
 is the moment of inertia
is the moment of inertia
and
 is the angular velocity
is the angular velocity
The translational kinetic energy
 is given by
is given by
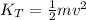
Where
 is the mass
is the mass
and
 is the translational speed (velocity)
is the translational speed (velocity)
∴
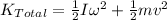
But, the moment of inertia
 of a sphere is given by
of a sphere is given by

Where
 is mass
is mass
and
 is radius
is radius
∴
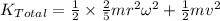
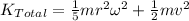
Also,
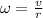
∴
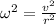
Then,
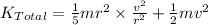
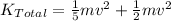
∴

From the question,
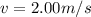
Then,

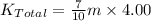
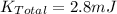
Hence, the total kinetic energy is 2.8m J. (NOTE: m is mass of the sphere)