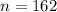Complete Question
In a sample of 80 light bulbs, the mean lifetime was 1217 hours with a standard deviation of 52 hours. a. Find the 95% confidence interval for the mean lifetime of this type of bulb. Justify the reason you chose the distribution used to construct the confidence interval. b. How many light bulbs must be sampled so that a 95% confidence interval will specify the mean lifetime to within
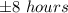 ?
?
Answer:
a
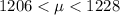
The reason why a normal distribution was chosen is because the sample size is large enough that is
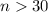
b
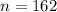
Explanation:
From the question we are told that
The sample size is n = 80
The sample mean is
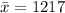
The standard deviation is
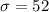
From the question we are told the confidence level is 95% , hence the level of significance is
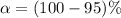
=>

Generally from the normal distribution table the critical value of is
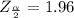
Generally the margin of error is mathematically represented as
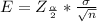
=>
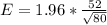
=>
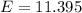
Generally 95% confidence interval is mathematically represented as
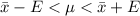
=>
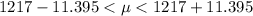
=>
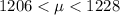
Generally the sample size is mathematically represented as
![n = [\frac{Z_{(\alpha )/(2) } * \sigma }{E} ] ^2](https://img.qammunity.org/2021/formulas/mathematics/college/j63im5d7bkeqfrgf56wd02g4fvud45p15n.png)
Here E = 8
=>
![n = [(1.96 * 52 )/(8) ] ^2](https://img.qammunity.org/2021/formulas/mathematics/college/u7b2imfaffz3v57vxt96czatwiqurfhd71.png)
=>