Question

laser beam is incident on two slits with a separation of 0.195 mm, and a screen is placed 5.10 m from the slits. If the bright interference fringes on the screen are separated by 1.61 cm, what is the wavelength of the laser light?

Answer 1

615 nm

Step-by-step explanation:

The separation between the two slits, d = 0.195 mm =
`0.195* 10^(-3)\ m`

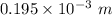
The bright interference fringes on the screen are separated by 1.61 cm,
`\Delta y=1.61\ cm=0.0161\ m`

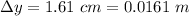
Distance between the screen and the slit, D = 5.1 m

We need to find the wavelength of the laser light. The separation between two bright interference fringes is given by:

`\Delta y=(\lambda D)/(d)\\\\\lambda=(\Delta y d)/(D)\\\\=(0.0161* 0.195* 10^(-3))/(5.1)\\\\=6.15* 10^(-7)\ m\\\\=615\ nm`

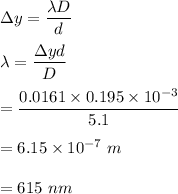
So, the wavelength of the laser light is 615 nm.