Question

A population grows exponentially at the rate of 1.35%. How long (in years) will it take the population to double?

Answer 1

Answer: Approximately 51 years.

Explanation: A population grows by changing exponentially over time, which can be mathematically demonstrated as:

`P=P_(0)e^(rt)`

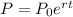
where

P is the population after time

P₀ is initial population, when time = 0

r is a percentage rate of growth

t is time passed

In this case, we have to calculate the amount of time it has passed for a population to double, so
`P=2P_(0)`:

`2P_(0)=P_(0)e^(0.0135t)`

`e^(0.0135t)=2`

`ln(e^(0.0135t))=ln2`

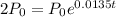
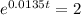
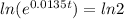
Using Logarithm Rule
`ln(e^(k))=k`:

`0.0135t=0.693`

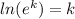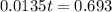
t = 51.34

For a population with rate of 1.35%, it will take approximately 51 years to double.