Answer:
Diameter of the piston would be 0.71 m (71.1 cm)
Step-by-step explanation:
From the principle of pressure;
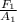 =
=
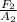
Let
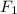 = 2903.57 lb,
= 2903.57 lb,
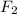 = 24.41 lbs,
= 24.41 lbs,
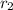 = 3.26 cm = 0.0326 m.
= 3.26 cm = 0.0326 m.
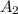 =
=
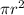
=
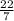 x
x
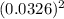
= 0.00334
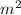
So that:
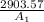 =
=
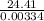
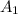 =
=
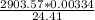
= 0.3973
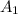 = 0.4
= 0.4
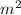
The radius of the piston can be determined by:
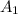 =
=
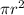
0.3973 =
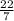 x
x
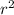
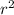 =
=
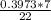
= 0.1264
r =
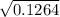
= 0.3555
r = 0.36 m
Diameter of the piston = 2 x r
= 2 x 0.3555
= 0.711
Diameter of the piston would be 0.71 m (71.1 cm).