Solution:
Given that :
Volume flow is,
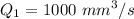
So,
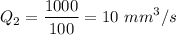
Therefore, the equation of a single straight vessel is given by
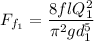 ......................(i)
......................(i)
So there are 100 similar parallel pipes of the same cross section. Therefore, the equation for the area is
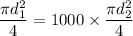
or
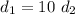
Now for parallel pipes
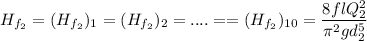 ...........(ii)
...........(ii)
Solving the equations (i) and (ii),
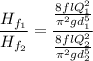

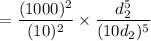
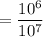
Therefore,
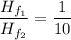
or
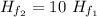
Thus the answer is option A). 10