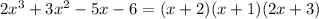Question

Let g be a polynomial function of x where g(x) = 2x^3+ 3x^2-5x-6 . If (x+2) is a factor of g, write an equation for g as the product of linear factors

Answer 1

`2x^3+ 3x^2-5x-6 = (x+2)(x+1)(2x+3)`

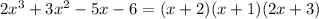
Explanation:

Given polynomial
`g`:

`g(x) = 2x^3+ 3x^2-5x-6`

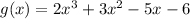
A factor of polynomial is
`(x+2)`.

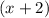To find:

Equation of the polynomial as the product of linear factors.

Solution:

First of all, let us divide the polynomial
`g` with
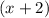`(x+2)` to find the other factors.

As degree of polynomial is 3, when divided by a linear equation, it will result in a quadratic.

That quadratic will have 2 solutions.

Solving the quadratic in linear will give us the answer.

Result of division:

`(2x^3+ 3x^2-5x-6)/(x+2) =2x^2-x-3`

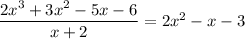
Now, solving the quadratic:

`2x^2-x-3 = 2x^2-3x+2x-3 \\\Rightarrow x(2x-3)+1(2x-3)\\\Rightarrow (x+1)(2x-3)`

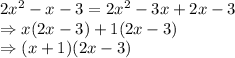
So, the linear equation can be written as:

`2x^3+ 3x^2-5x-6 = (x+2)(x+1)(2x+3)`