Question

Considere la siguiente ecuación: 16a – ( 3a – (6 – 9a) ) = 30a + ( – (3a + 2) – (a + 3) ) III) Al romper paréntesis, agrupar términos semejantes y simplificar. La ecuación queda:

Answer 1

La ecuación simplificada es
`a = (11)/(19)`.

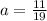Explanation:

Tenemos la siguiente ecuación simultánea:
`16\cdot a - [3\cdot a - (6-9\cdot a)] = 30\cdot a +[-(3\cdot a+2)-(a+3)]`. El procedimiento consiste en destruir los paréntesis desde dentro hacia fuera, agrupar los términos semejantes y simplificar. Presentamos el proceso paso por paso:

1)
`16\cdot a - [3\cdot a - (6-9\cdot a)] = 30\cdot a +[-(3\cdot a+2)-(a+3)]` Dado

2)
`16\cdot a -\{3\cdot a + (-1)\cdot [6+(-1)\cdot 9\cdot a]\} = 30\cdot a +\{(-1)\cdot (3\cdot a +2)+(-1)\cdot (a+3)\}`
`-b = (-1)\cdot b`

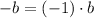
3)
`16\cdot a -\{[(-1)\cdot (6)+(-1)\cdot (-1)\cdot 9\cdot a]\}= 30\cdot a +\{\left[(-1)\cdot (3\cdot a) + (-1)\cdot (2)\right] +[(-1)\cdot a +(-1)\cdot (3)] \}` Propiedad distributiva

4)
`16\cdot a -(-6+9\cdot a) = 30\cdot a +(-3\cdot a -2-a-3)`
`-b = (-1)\cdot b`/
`(-b)\cdot (-c) = b\cdot c`

5)
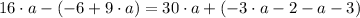
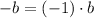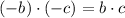
`16\cdot a +(-1)\cdot (-6+9\cdot a) = 30\cdot a -4\cdot a-5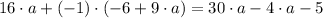` Propiedad distributiva/Definiciones de adición y sustracción/
`-b = (-1)\cdot b`

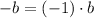
6)
`16\cdot a +[(-1)\cdot (-6)+(-1)\cdot (9\cdot a)] = 26\cdot a -5` Propiedad distributiva/Definiciones de adición y sustracción/Propiedad modulativa.

7)
`16\cdot a +6-9\cdot a = 26\cdot a - 5`
`-b = (-1)\cdot b`/
`(-b)\cdot (-c) = b\cdot c`

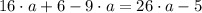
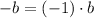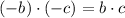
8)
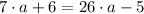`7\cdot a +6 = 26\cdot a - 5` Propiedad distributiva/Definiciones de adición y sustracción.

9)
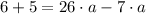`6+5 = 26\cdot a -7\cdot a` Compatibilidad con la adición/Definición de sustracción.

10)
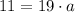`11 = 19\cdot a` Propiedad distributiva/Definiciones de adición y sustracción.

11)
`19\cdot a = 11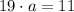` Simetría de la igualdad.

12)
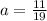`a = (11)/(19)` Compatibilidad con la multiplicación/Existencia del inverso multiplicativo/Propiedad modulativa/Definición de división/Resultado.

La ecuación simplificada es
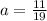`a = (11)/(19)`.