Question

A Boy has a ball and throws it straight up into the air with an initial velocity of 6 m/s. Calculate the maximum height of the ball and the time the ball is in the air.

Answer 1

i. 1.84 m

ii. The ball's time in the air is 1.23s.

Step-by-step explanation:

The ball moves upward (against the gravitational pull) with an initial velocity of 6 m/s.

I. Applying the third equation of free fall, the maximum height is;

`V^(2)` =
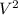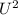`U^(2)` - 2gs

where the variables have there usual meaning.

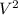`V^(2)` = 0 m/s,
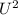`U^(2)` = 6 m/s, g = 9.8 m/
`s^(2)`.

0 =
`6^(2)` - 2 x 9.8 x s

0 = 36 - 19.6s

⇒ 19.6s = 36

s =
`(36)/(19.6)`

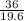
= 1.8367

= 1.84 m

The maximum height of the ball is 1.84 m.

II. The time the ball was in air can be determined by,

time of flight, T =
`(2USin A)/(g)`

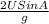
where U is the initial velocity of the ball, A is the angle of projection and g is the acceleration due to gravity.

U = 6 m/s, A =
`90^(o)` (since the ball is thrown vertically upward), and g = 9.8 m/
`s^(2)`.

T =
`(2 *6 Sin90^(o) )/(9.8)`

=
`(12)/(9.8)`

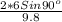
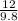
= 1.2245

T = 1.23s

The ball's time in the air is 1.23s.