Question

A pitcher's arm rotates at a speed of 777 degrees per millisecond \left( \dfrac{\text{degrees}}{\text{ms}} \right)(

ms

degrees

​

)left parenthesis, start fraction, start text, d, e, g, r, e, e, s, end text, divided by, start text, m, s, end text, end fraction, right parenthesis.

At what speed does the pitcher's arm rotate in \dfrac{\text{degrees}}{\text{s}}

s

degrees

​

start fraction, start text, d, e, g, r, e, e, s, end text, divided by, start text, s, end text, end fraction?

Answer 1

7000degrees/sec

Explanation:

The question is not properly structured. Here is the correct question.

A pitcher's arm rotates at a speed of 7 degrees per millisecond (degrees/ms) . At what speed does the pitcher's arm rotate in degrees/s?

Before we proceed, you must know that we will be applying the following conversion;

1 milliseconds = 10⁻³secs

Given

Speed of pitcher's arm in degree per milliseconds = 7deg/ms

Required

We are to express in degree/sec

Using the conversion formula above;

`7deg/ms = (7^0)/(1millisecs) \\\\converting \ to \ deg/s\\7deg/ms = (7^0)/(1millisecs) * (1)/(10^(-3)s)\\7deg/ms = (7^0)/(10^(-3)s)\\`

`7deg/ms = 7^0 * 1/0.001s\\7deg/ms = 7^0 * 1000/s\\7deg/ms = 7000^0/sec\\`

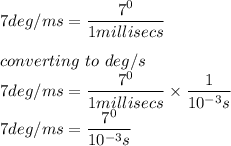
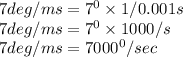
Hence the value in degree/sec is 7000degrees/sec