Question

A family has two cars. During one particular week, the first car consumed 40 gallons of gas and the second consumed 15 gallons of gas. The two cars drove a combined total of 1575 miles, and the sum of their fuel efficiencies was 55 miles per gallon. What were the fuel efficiencies of each of the cars that week?

Answer 1

Fuel efficiency of first car = 30 miles/gallon

Fuel efficiency of second car = 25 miles/gallon

Explanation:

Given that:

Fuel consumed by first car = 40 gallons

Fuel consumed by second car = 15 gallons

Total distance drove by the two cars combined = 1575 miles

Sum of their fuel efficiencies = 55 miles/gallon

To find:

The fuel efficiencies of each of the cars = ?

Solution:

Fuel efficiency of a car is defined as the ratio of distance traveled in miles to the number of gallons used by the car.

Let the distance traveled by first car =
`x` miles

So, the distance traveled by other car = (1575 -
`x`) miles

Fuel efficiency of first car =
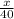`(x)/(40)` miles/gallon

Fuel efficiency of second car =
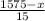`(1575-x)/(15)` miles/gallon

As per given question statement:

`(x)/(40)+(1575-x)/(15)=55\\\Rightarrow 15x+1575* 40-40x=55* 40 * 15\\\Rightarrow 25x=30000\\\Rightarrow x =1200\ miles`

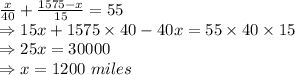
Distance traveled by first car = 1200 miles

Fuel used by first car = 40 gallons

So, fuel efficiency of first car =
`(1200)/(40) = \bold{30\ miles/gallon}`

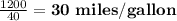
Distance traveled by second car = 1575 - 1200 = 375 miles

Fuel used by second car = 15 gallons

So, fuel efficiency of second car =
`(375)/(15) = \bold{25\ miles/gallon}`