Answer:

Explanation:
Given dimensions:
- Radius of the cylinder = 7 metres
- Height of the cylinder = 3 metres
Given value of π :
To find:
- The Volume of the cylinder
Solution:
Here, we'll need to use the formulae of the volume of cylinder,to find it's volume.Its actually like a savior while solving these type of questions.

where,
- π = 3.14
- r² = (radius)²
- h = height
Plug/substitute them onto the formulae,then simplify it using PEMDAS.
- [We'll substitute the value of π later]
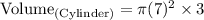
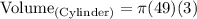
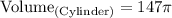
- Now substitute the value of π.
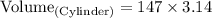
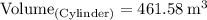

Hence, we can conclude that:
The volume of the cylinder is approximately
461.6 m³.
