Question

At the candy shop, Ameenah sells chocolate covered raisins, c, for $1.50 per pound, and peanuts, p, for $1.20 per pound. Ameenah wants to make 20 pounds of a mixture of raisins and peanuts that sells for $1.35 a pound. How many pounds of each should she use?

Thanks! :)

Answer 1

10 pounds of both raisins and peanuts.

Explanation:

Answer 2

10 pounds of raisins and 10 pounds of peanuts.

Explanation:

Let c represent the pounds of chocolate covered raisins.

Let p represent the pounds of peanuts.

We know that the raisins cost $1.50 per pound and the peanuts cost $1.20 per pound.

Ameenah wants to make 20 pounds of a mixture of the raisins and peanuts that sells for 1.35 a pound. So, we can write the following expression:

`1.5c+1.2p`

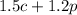
This represents the cost given c pounds of raisins and p pounds of peanuts.

Ameenah wants to combine c and p to make them 1.35 per pound. In other words, the expression must equal:

`1.5c+1.2p=1.35(c+p)`

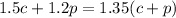
We also know that she wants to make 20 pounds. So, c plus p must total 20. Therefore:

`c+p=20`

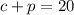
We now have the system of equations:

`\left\{ \begin{array}{ll} 1.5c+1.2p=1.35(c+p) \\ c+p=20\end{array}`

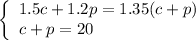
First, since we know that c+p is 20, we can substitute that into the first equation.

Second, let's subtract p from both side for the second equation to isolate a variable. So:

`c=20-p`

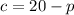
Let's now substitute this into the first equation:

`1.5(20-p)+1.2p=1.35(20)`

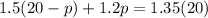
Distribute:

`30-1.5p+1.2p=27`

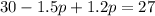
Combine like terms:

`-0.3p+30=27`

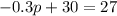
Subtract 30 from both sides:

`-0.3p=-3`

Divide both sides by -0.3. So, the amount of peanuts needed is:

`p=10`

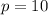
10 pounds of peanuts is needed.

This means that 20-10 or 10 pounds of raisins is needed.