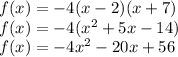Answer:
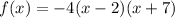
Or, in standard form:

Explanation:
We can use the factored form of a quadratic equation:
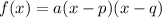
Where a is the leading coefficient and p and q are the zeros of the quadratic.
We know that the x-intercepts are at (2, 0) and (-7, 0).
So, let's substitute 2 for p and -7 for q. This yields:
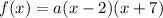
Now, we need to determine a.
We know that it passes through the point (1, 32). In other words, if we substitute 1 for x, we should get 32 for f(x). Therefore:

We can now solve for a. First, compute:
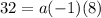
Multiply:
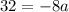
Divide both sides by -8:
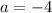
So, the value of a is -4.
Therefore, our entire equation is:
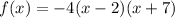
Notes:
We can expand this into standard form: