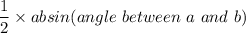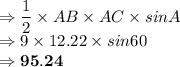Answer:
Perimeter = 32.3
Area = 95.24
Explanation:
Given:
△ABC, m∠A=60°
m∠C=45°, AB = 9
To find:
Perimeter of △ABC
Area of △ABC
Solution:
Using angle sum property in a triangle:
m∠A + m∠B + m∠C = 180°
m∠B = 180° - 45° - 60° = 75°
As per Sine Rule:

Where
 is the side opposite to
is the side opposite to

 is the side opposite to
is the side opposite to
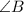
 is the side opposite to
is the side opposite to

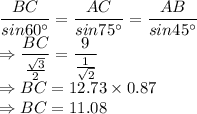

Perimeter of △ABC = AB + BC + AC = 9 + 11.08 + 12.22 = 32.3
Area of a triangle is given as: