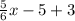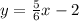Question

Write an equation of the line passing through the point (6, 3) that is perpendicular to the line 6x + 5y = 10

An equation of the line is
y=?

Answer 1

`y=(5)/(6)x-2`

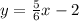
Explanation:

Let the equation of a line passing through a point
`(x_1,y_1)` and slope
`m_1` is,

`y-y_1=m_1(x-x_1)`

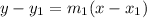
Equation of the second line has been given as,

6x + 5y = 10

Slope-intercept form of the equation will be,

5y = -6x + 10

y =
`-(6)/(5)x+10`

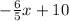
Here slope of the line
`m_2=-(6)/(5)`

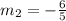
If both the lines are perpendicular,

By the property of perpendicular lines,

`m_1* m_2=-1`

`m_1* (-(6)/(5))=-1`

`m_1=(5)/(6)`

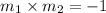
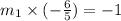
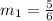
Therefore, equation of the line passing through (6, 3) and slope =
`(5)/(6)` will be,

y - 3 =
`(5)/(6)(x-6)`

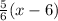
y =
`(5)/(6)x-5+3`

`y=(5)/(6)x-2`