Question

Find the equation of the line.

The perpendicular bisector to the line segment with endpoints (-8,5) and (4,1).
The equation of the line is
y =

Answer 1

y = 3x + 9

Explanation:

The perpendicular bisector to the line segment is passing through the midpoint of the line segment. Coordinates of midpoint are (
`(x_(1) +x_(2) )/(2)` ,
`(y_(1) +y_(2) )/(2)` )

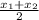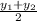Formula of slope is m =
`(y_(2) -y_(1) )/(x_(2) -x_(1) )`

Slopes of perpendicular lines are opposite reciprocals. So, if AB ⊥ CD , then
`m_(AB)` ×
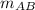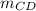`m_(CD)` = - 1

y -
`y_(1)` = m ( x -
`x_(1)` )

~~~~~~~~~~~

(- 8, 5)

(4, 1)

m = ( 5 - 1) / ( - 8 - 4) = -
`(1)/(3)`

Opposite reciprocal to ( -
`(1)/(3)` ) is 3

Coordinates of midpoint are ( - 2 , 3 )

y - 3 = 3 ( x + 2 )

y = 3x + 9