![~~~~~~~~~~~~\textit{function transformations} \\\\\\ f(x)=Asin(Bx+C)+D \qquad \qquad f(x)=Acos(Bx+C)+D \\\\ f(x)=Atan(Bx+C)+D \qquad \qquad f(x)=Asec(Bx+C)+D \\\\[-0.35em] ~\dotfill\\\\ \bullet \textit{ stretches or shrinks}\\ ~~~~~~\textit{horizontally by amplitude } A\cdot B\\\\ \bullet \textit{ flips it upside-down if }A\textit{ is negative}\\ ~~~~~~\textit{reflection over the x-axis} \\\\ \bullet \textit{ flips it sideways if }B\textit{ is negative}\\ ~~~~~~\textit{reflection over the y-axis}](https://img.qammunity.org/2023/formulas/mathematics/high-school/vdbtty4s81fupybxkca2pbdjmak2nzuqx8.png)

with the template above in mind, let's check the graph of that function, it has a midline at y = 0, namely the x-axis, so it has the same midline as sine, we'll use sine, because sine graph starts at 0 and then it moves up and then down, this one starts at 0, reason why, I guess we could also use a -cosine, which has the same effect, anyhow, let's use sine.
from the midlne up, we have a peak at 1.5 or 3/2 which our Amplitude.
we can also see that from 0 to 8, is the graph, after that it simply repeats, so we can say that the period of that one is 8, thus
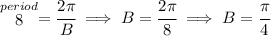
and since the midline is same as sin(θ) that means it doesn't have a vertical shift, so our D = 0, and since it's beginning at x = 0, it doesn't have any horizontal shift from the sin(θ) either, so C = 0, thus we can write it as
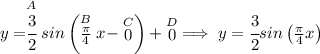
Check the picture below.