Question

Givin the standard form for a trinomial ax^2+bx+c, and factored form (px+r)(qx+s) match the following:

a=
b=
c=
to
(p*s)+(q*r)
r*s
p*q

Answer 1

`a = p*q\\b = (p*s)+(q*r)\\c = r*s`

Explanation:

We are given the standard form of trinomial

`ax^2+bx+c`

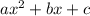
After factorization, the form is:

`(px+r)(qx+s)`

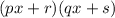
We have to compare the factored form and the standard form to find the values of a,b and c in terms of p,q,r and s. For this purpose, the factored form will be converted into standard form.

Multiplying the both factors

`(px+r)(qx+s)\\=px(qx+s)+r(qx+s)\\= pqx^2+psx+qrx+rs\\= pqx^2+(ps+qr)x+rs`

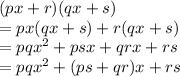
Comparing both forms with each other

After comparing

`a = pq = p*q\\b = ps+qr = (p*s)+(q*r)\\c = rs = r*s`

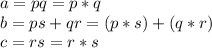
Hence,

`a = p*q\\b = (p*s)+(q*r)\\c = r*s`