Question

Find the equation of the line that is perpendicular to the given line and passes through the given point.

y = − 1/6x − 5; (14, 0)

The equation is y =______.

Answer 1

The equation is y =6x-84.

Explanation:

We need to find the equation of the line that is perpendicular to the given line and passes through the given point.

y = − 1/6x − 5; (14, 0)

Slope of required line

The equation of given line
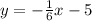`y = - (1)/(6) x - 5` is in slope-intercept form.

Comparing it with general formula of slope-intercept form
`y=mx+b` where m is slope and b is y-intercept. The slope of line m is: -1/6

So, the slope of required line that is perpendicular to given line is 6 because the equation of line that we need to find is perpendicular to the given line, so their slopes will be:
`m_1=-(1)/(m_2)`

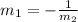
So, slope = 6

Finding y-intercept of required line

Using slope =6 and point (14,0) we can find y-intercept of required line by slope-intercept formula

`y=mx+b\\0=6(14)+b\\0=84+b\\b=-84`

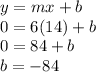
Equation of required line:

The equation of required line having slope (m)= 6 and y-intercept (b)= -84 is:

`y=mx+b\\y=6x-84`

The equation is y =6x-84.