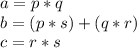Answer:
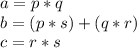
Explanation:
The standard form of trinomial is given as:
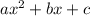
And the factored form is:
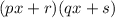
In order to find the values of a,b and c in terms of p,q,r and s we will take the factored form, multiply it and then compare it with the standard form.
So,
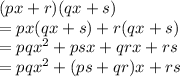
Now comparing it with the standard form of trinomial
We will compare the co-efficients of x^2, x and the constant
By comparing, we get
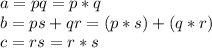
Hence,