Question

HELP! help is needed ASAP! help is very much appreciated.

Answer 1

Length of side e is 4.12

Length of side f is 4.24

The length of side f is larger than length of side e

Explanation:

We are given two line segments e and f. We need to find lengths of both e and f and determine which is larger.

We can use distance formula to calculate lengths of line segments.

The Distance Formula is:
`√((x_2-x_1)^2+(y_2-y_1)^2)`

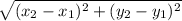
Finding length of side e:

We are given points (-2,3) and (-1,-1)

here we have
`x_1=-2, y_1=3, x_2=-1 , y_2=-1`

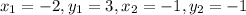
Putting values in distance formula and finding length

`Length \ of \ side \ e= √((x_2-x_1)^2+(y_2-y_1)^2)\\Length \ of \ side \ e= √(((-1)-(-2))^2+(-1-(3))^2)\\Length \ of \ side \ e= √((-1+2)^2+(-1-3)^2)\\Length \ of \ side \ e= √((1)^2+(-4)^2)\\Length \ of \ side \ e= √(1+16)\\Length \ of \ side \ e= √(17)\\Length \ of \ side \ e= 4.12`

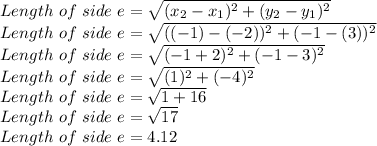
So, Length of side e is 4.12

Finding length of side f:

We are given points (2,2) and (-1,-1)

here we have
`x_1=2, y_1=2, x_2=-1 , y_2=-1`

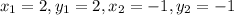
Putting values in distance formula and finding length

`Length \ of \ side \ f= √((x_2-x_1)^2+(y_2-y_1)^2)\\Length \ of \ side \ f= √(((-1)-(2))^2+(-1-(2))^2)\\Length \ of \ side \ f= √((-1-2)^2+(-1-2)^2)\\Length \ of \ side \ f= √((-3)^2+(-3)^2)\\Length \ of \ side \ f= √(9+9)\\Length \ of \ side \ f= √(18)\\Length \ of \ side \ f= 4.24`

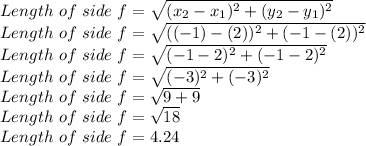
So, Length of side f is 4.24

The length of side f is larger than length of side e