Answer:
-14
Explanation:
I might be wrong, but this is my interpretation of the problem.
To solve this problem, find the endpoints of the line in the interval. Then draw a line between those two points. Finally, find the slope of the line that passes between the two points.
The line is f(x) = -2x^(2) + 2x + 1
The interval (in standard notation) is (3
 x
x
 5)
5)
So when x = 3,
-2x^(2) + 2x + 1
-2(3)^(2) + 2*3 + 1
-2 * 9 + 6 + 1
-18 + 7
- 11
One endpoint is: (3, -11).
When x = 5
-2x^(2) + 2x + 1
-2(5)^2 + 2*5 + 1
-2 * 25 + 10 + 1
-50 + 11
-39
The other endpoint is; (5, -39).
Find the slope of a line passing through these two points.
The formula to find the slope of a line is:
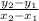
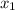 = 3
= 3
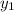 = -11
= -11
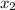 = 5
= 5
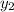 = -39
= -39
((-39) - ( -11))/((5) - (3))
Simplify
-28/2
-14