Question

(-2,8), (r, 4), m =-1/2

Answer 1

`r=6`

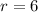
Explanation:

Make an equation in point-slope form where:

• the equation is
  `y-y_(1)=m(x-x_(1))`

• m is the slope

• y1 and x1 are the corresponding coordinate points
  `(x_(1),y_(1))`

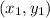
Insert the known values:

`(-2_(x1),8_(y1))\\\\m=-(1)/(2) \\\\y-8=-(1)/(2) (x-(-2))\\\\y-8=-(1)/(2) (x+2)`

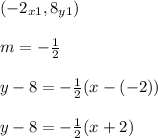
Use the distributive property:

`-(1)/(2) (x+2)\\\\-(1)/(2)(x)-(1)/(2)(2)`

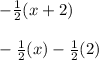
Simplify. Turn the 2 into a fraction by converting to the fraction
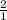`(2)/(1)` , which is still equal to 2:

`-(1)/(2)(2)\\\\-(1)/(2)*(2)/(1)`

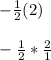
Multiply across:

`-(1)/(2)*(2)/(1) =-(2)/(2) =-1`

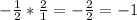
Re-insert into the equation:

`y-8=-(1)/(2)x-1`

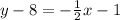
Solve for y. Add 8 to both sides (to isolate y using inverse operations):

`y-8+8=-(1)/(2)x-1+8\\\\y=-(1)/(2)x+7`

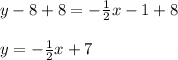
Now insert the y value of the other point to find r (which will have the same value as x):

`(r_(x),4_(y))\\\\4=-(1)/(2)x+7`

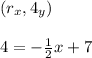
Simplify the fraction by multiplying. Add 1 as the denominator for x:

`-(1)/(2)*(x)/(1)`

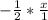
Multiply across:

`-(1)/(2)*(x)/(1)=-(x)/(2)`

Re-insert:

`4=-(x)/(2) +7`

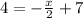
Subtract 7 from both sides (to isolate the variable using inverse operations):

`4-7=-(x)/(2) +7-7\\\\-3=-(x)/(2)`

Multiply both sides by 2 (to undo the fraction using inverse operations):

`2(-3)=2(-(x)/(2)) \\\\-6=-x`

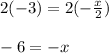
Divide both sides by -1 (to make the variable positive, since two negatives make a positive):

`(-6)/(-1) =(-x)/(-1) \\\\x=6`

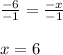
Therefore, the value of r is 6.

:Done