Answer:
Parent function
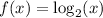
Since we cannot take logs of zero or negative numbers, the domain is
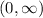 and there is a vertical asymptote at
and there is a vertical asymptote at
 .
.
There are no horizontal asymptotes and the range is
 .
.
The end behaviors of the parent function are:
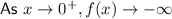
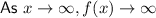
To determine the attributes of the given function, compare the given function with the parent function.
Given function
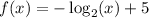
The given function is reflected in the x-axis. Therefore, the end behaviors are a reflection of those of the parent function:
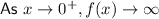
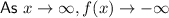
As the given function is translated vertically (5 units up) only, the domain, range and asymptote will not change, since the function has not been translated horizontally.


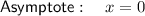
Conclusion
The function f(x) is a
 function with a
function with a
 asymptote of
asymptote of
 .
.
The range of the function is
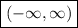 , and it is
, and it is
 on its domain of
on its domain of
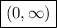 .
.
The end behavior on the LEFT side is as
 ,
,
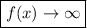 , and the end behavior of the RIGHT side is
, and the end behavior of the RIGHT side is
 ,
,
 .
.