Question

What is the length of segment DF?

B
4/28
1
68°
C
2
А A
2
3
8
4
68°
28°
F
5
Type your answer.

Answer 1

DF = 17.12

Explanation:

From the picture attached,

From ΔABC and ΔEFD,

m∠ABC = m∠EFD = 28°

m∠BAC = m∠EDF = 68°

By AA property of similarity, ΔABC and ΔEFD will be similar.

And their corresponding sides will be proportional.

`(AB)/(EF)=(BC)/(DF)=(AC)/(ED)`

`(4)/(EF)=(BC)/(DF)=(2)/(8)`

`(4)/(EF)=(1)/(4)`

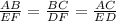
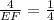
EF = 16

Now by applying cosine rule in ΔDEF,

DF² = ED² + EF² - 2(ED)(EF)cos(E)

DF² = 8² + (16)² - 2(8)(16)cos(84)°

DF² = 320 - 26.76

DF = √(293.24)

DF = 17.12