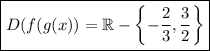Question

Find f(g(x)). State the domain of the composite function.

f(x) = 3x-2/x+1
g(x) = x+5/2x-3

Answer 1

ℝ - {(-2/3),(3/2)}

Explanation:

We want the domain of f(g(x)). So, firstly, we have to find the domain for g(x) and, then, for f(g(x)).

- Domain of g(x): Since the expression is a fracion, we must exclude the values of x that make null the denominator. Hence,

`g(x)=(x+5)/(2x-3)\Longrightarrow 2x-3\\eq 0\iff \boxed{x\\eq(3)/(2)}`

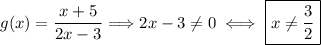
- Domain of f(g(x)): We'll find its expression:

`f(x) = (3x-2)/(x+1)\\\\f(g(x)) = (3g(x)-2)/(g(x)+1)\\\\f(g(x)) = (3\cdot(x+5)/(2x-3)-2)/((x+5)/(2x-3)+1)=(~~~(3(x+5)-2(2x-3))/(2x-3)~~~)/(((x+5)+(2x-3))/(2x-3))\\\\f(g(x)) =(3(x+5)-2(2x-3))/((x+5)+(2x-3))=(3x+15-4x+6)/(x+5+2x-3)\\\\\boxed{f(g(x)) =(21-x)/(3x+2)}`

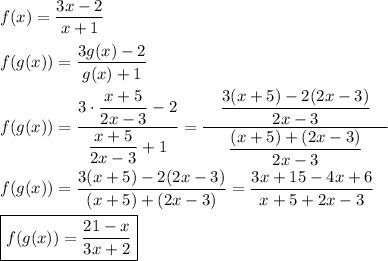
Now, once again, we have to exclude the values of x that make the denominator equals to zero. Thus,

`f(g(x)) =(21-x)/(3x+2)\Longrightarrow 3x+2\\eq0\iff \boxed{x\\eq-(2)/(3)}`

Lastly, we may write the domanin of f(g(x)):

`D(f(g(x)) = \left]-\infty,-(2)/(3)\right[\cup\left]-(2)/(3),(3)/(2)\right[\cup\left](3)/(2),\infty\right[`

or, just writing in a shorter way:

`\boxed{D(f(g(x)) = \mathbb{R}-\left\{-(2)/(3),(3)/(2)\right\}}`