Question

Orchestra Tonight is selling tickets for its local performance. Orchestra fans can buy tickets to sit in the balcony or on the floor of the concert hall. Tickets for floor seats are $83 each. Tickets for the balcony are 60% of the price of the floor tickets. Which inequality represents all possible combinations of f, the number of tickets for floor seats, and b, the number of tickets for balcony seats, that a person can buy and spend no more than $560?

Answer 1

`83f+49.8b \leq 560`

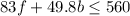
Explanation:

Given that the cost of 1 floor ticket = $ 83.

Cost for f floor tickets = $ 83f

Ticket for 1 balcony ticket = 60% of floor ticket.

= 0.60 x 83 = $49.8

Cost for b balcony tickets = $ 49.8b.

Total cost for f floor tickets and b balcony tickets, C= 83f+49.8b.

As the person can spend a maximum of $560,

So,
`C\leq 560`

`\Rightarrow 83f+49.8b \leq 560`.

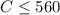
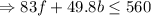Hence, the required inequality is
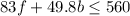`83f+49.8b \leq 560`.