Answer:
Approximately
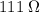 .
.
Step-by-step explanation:
It is given that
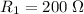 and
and
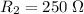 are connected in a circuit in parallel.
are connected in a circuit in parallel.
Assume that this circuit is powered with a direct current power supply of voltage
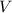 .
.
Since
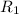 and
and
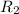 are connected in parallel, the voltage across the two resistors would both be
are connected in parallel, the voltage across the two resistors would both be
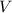 . Thus, the current going through the two resistors would be
. Thus, the current going through the two resistors would be
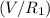 and
and
 , respectively.
, respectively.
Also because the two resistors are connected in parallel, the total current in this circuit would be the sum of the current in each resistor:
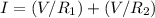 .
.
In other words, if the voltage across this circuit is
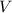 , the total current in this circuit would be
, the total current in this circuit would be
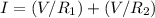 . The (equivalent) resistance
. The (equivalent) resistance
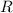 of this circuit would be:
of this circuit would be:
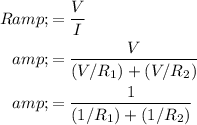 .
.
Given that
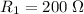 and
and
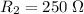 :
:
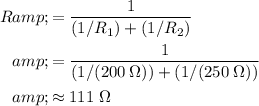 .
.