If we evaluate the function at infinity, we can immediately see that:
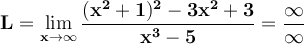
Therefore, we must perform an algebraic manipulation in order to get rid of the indeterminacy.
We can solve this limit in two ways.
Way 1:
By comparison of infinities:
We first expand the binomial squared, so we get
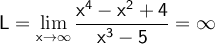
Note that in the numerator we get x⁴ while in the denominator we get x³ as the highest degree terms. Therefore, the degree of the numerator is greater and the limit will be \infty. Recall that when the degree of the numerator is greater, then the limit is \infty if the terms of greater degree have the same sign.
Way 2
Dividing numerator and denominator by the term of highest degree:
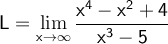
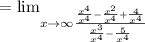
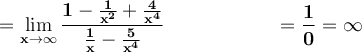
Note that, in general, 1/0 is an indeterminate form. However, we are computing a limit when x →∞, and both the numerator and denominator are positive as x grows, so we can conclude that the limit will be ∞.